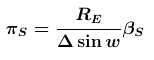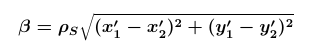The Transit of Mercury 2019: Basic Ideas
| 1. | 2. | 3. | 4. |
 |
 |
 |
 |
Caracas, Venezuela, 14:00:00 UT
(E. Torres) |
Hannover, Germany, 14:00:01 UT
(U. Backhaus) |
Caracas
rescaled and rotated |
Hannover
clipped and rotated |
We visualize the procedure graphically with two transit photos of 2016: On the original images the sun has different size and orientation (1. and 2.). Therefore, the Caracas image has been rotated and rescaled (3.) so that the radius of the sun is the same in both images. In the second step the Hannover image, too, has been rotated and clipped (4.). In order to get good quantitative results these steps have to be performed numerically.
The procedures of finding the direction to equatorial north are difficult. We will describe them later.
 |
|---|
Combination ("max") of the suitable rotated and rescaled 14:00 UT images from Caracas and Hannover
Mercury's parallax is really small. |
If the angular radius of the sun is known or can be measured, the angle of parallax
β can be measured in this combinated image.
back to top
The parallax effect describes the effect that a celestial object has slightly different positions with respect to the much farer stars when be observed from different places on earth. That means that the directions from the both observers to the object are different. The angle
β between these directions is the so called parallax angle (or simply the parallax) of the object with respect to the both places. When the parallax is known the distance to the object can be determined.
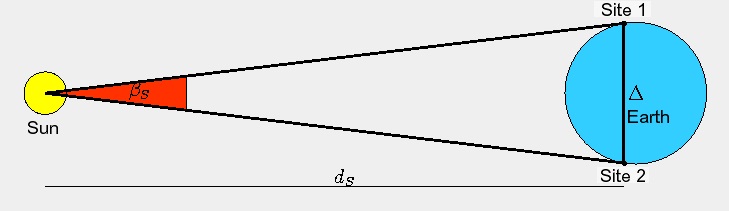

The transit of Mercury offers a possibility of measuring the distance to the sun by measuring the parallax of Mercury first. During a transit the solar disc serves as a reference system for position measurements. But there occurs a problem: The sun itself shows the parallactic effect.
Therefore, the parallactic shift β of Mercury with respect to the sun is not its angle of parallax βM.

Fortunately, this problem can be solved easily: Because the parallactic shift of the sun has the same direction as that of Mercury, the shift
β measured with respect to the solar disc is simply the difference of the parallaxes:
 | |
 |
When the observer moves from A to B,
Mercury and the sun shift into the same direction by βM and βS. | |
When the pictures of the sun are aligned,
the displacement of Mercury gets smaller by βS. |

Since Copernicus and Kepler the ratio of the radii of the planets (or, to be more precisely, the actual ratio of their distances to the sun) can be calculated without knowing the measure of the AU. Therefore, the parallax of Mercury
βM can be derived from the measured angle
β :

back to top
Now we are able to derive the angle of parallaxe of the sun, too:

or, even more simple:

And when we know this angle and the positions of the observers, we can derive the distance to the sun
dS:

The angle
βS - and therefore the distance
dS - depends on the projected linear distance
Δsin w between the observers. It is usual to refer the angle of parallax to the radius of the earth
RE. This angle then is simply called the
parallax of the sun πS or the solar parallax:
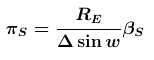
Because the parallactic shift is measured as a fraction
f of the sun's angular radius,
β=fρS, we get our final formulas for the solar parallax

and for the distance from the earth to the sun.

In this project, we will take as known the measures of (1) the earth's radius, (2) the sun's angular radius and (3) the ratio between the distances of the earth and Mercury from the sun. And different from the
transit project of 2004 we will not deal here with the determination of the projected distance between the corresponding observers
Δsin w.
Therefore, we will concentrate here on careful measurements of parallactic shifts β, i. e. of the ratio f.
back to top
We think that became clear in point 1. of this page that one essential problem of comparing simultaneously taken pictures from distant sites is
to determine their orientation, that means, for instance,
to determine the direction to equatorial north. There are, at least, three possibilities for handling this problem:
- Normally, the images made with well adjusted professional telescopes (with parallactic mounting or with azimutal mounting and a field de-rotator) need no processing because they are perfectly oriented.
- The direction from east to west is shown by the daily motion of celestial objects with (nearly) no proper motion. It can be found by taking two pictures with the camera fixed (autotracking switched off) with a time difference of about 2-4 minutes in a manner that the center of the solar disc can clearly be determined on both images. The displacement between the centers then shows the direction from east to west. The images below demonstrate the procedure: Two images taken with a time difference of 151s show the daily motion of the sun during that interval. The images can (but must not) be superimposed and the motion's direction can be determined by measuring the two positions of the solar center which here is done by adjusting circles to the sun's circumference with the little Windows-program evaltransitpicts. With respect to the east-west-direction the position of Mercury can be measured, for instance with the same program.
 |
 |
 |
 |
Hannover, 12:00:04
(U. Backhaus) |
Hannover, 12:02:35
(U. Backhaus) |
Hannover, 12::00:04 + 12:02:35
(max-combination) |
Hannover, 12::00:04 + 12:02:35
(Measurement of Mercury's positions) |
-
If an observer took only one image of the sun at a certain time which doesn't indicate the precise orientation of the sun one needs to find a prominent and sharp spot on the solar disc. This allows to measure Mercury's position with respect to that sun spot (see below) or to orient the image (for instance, by comparing it with the simultaneously taken image of the SDO). Because of the smaller distance between the center and the spot this method is by far less acurate than the above one.
The images below demonstrate the procedure: Two simultaneously taken pictures are roughly, but not exactly oriented. Therefore, in order to be able to compare the positions of Mercury they are measured with respect to the direction to a certain part of the most prominent sun spot which has been determined in advance (again using evaltransitpicts).
 |
 |
 |
 |
Pointe Saint Mathieu, 17:00:00
(T. Kunzemann) |
Jugendherberge Konstanz, 17:00:00
(Carl Bosch Gymnasium) |
Mercury's position angle with respect to the prominent sunspot |
back to top
Initially, we measure the pixel positions of the sun's center
(xS,yS) and of Mercury
(xM,yM) (
x to the west,
y to the north). The distance of Mercury
rM to the solar center then is:

In order to make measurements in differently sized pictures comparable we express lengths as fractions of the sun's pixel radius
rS:

With the relative coordinates
(xM-xS,y
M-y
S) Mercury's position angle
φ0 with respect to the lower edge of the image can be calculated. With the knowledge of the image's orientation this angle can be transformed into the correct position angle
φ which is measured counterclockwise from equatorial west (see above). Knowing
φ we are able to calculate Mercury's rectangular coordinates with respect to the westward direction:

Examples for this procedure are given in detail in our
exercises.
Finally, the parallactic shift
β of Mercury between two different pictures is
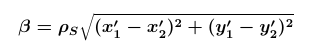
where
ρS is the angular radius of the sun.
Example
Correct orientation presupposed on the above superposition of the 14:00 pictures from Caracas and Hannover the following positions of Mercury can be measured:
x'1=-0.3712, y'1=-0.1891, x'2=-0.3643, y'2=-0.1937 and therefore β=0.00837ρS.
With the known values of the angular radius of the sun (15.84´) and of the geographical coordinates of the observers we find (with
comp2mercurypositions.xls, for instance) a not so bad measure of the solar parallax:
πS=8.3"
back to top
 |
 |
Editor: |
Udo Backhaus
 |
last update: 2019-04-03 |
 |