Final Results of the Project


(esta página en español)	(diese Seite auf deutsch)

Because of the very difficult weather conditions especially in Europe, but also in wide parts of South- and Northamerica, not as many participants as expected could observe the transit and contribute to the project with own images. But most of those who have uploaded images taken close to the proposed times followed the method of multiple expositioning in order to make it possible to precisely determine the orientation of their images. As a consequence, even images with bad seeing could be used to visualize the parallactic effect of Mercury in front of the sun.

Best results of single participants/groups

The pictures below represent the best results of those participants who have been able to take series of images which could be well aligned. Further results can be found on the page with "First results".
The images in the left column are originals in their original orientation. In order to be able to compare Mercury's position in front of the sun with that on an image taken at a distant place both images must have exactly the same orientation. In this project the east-west-direction of the images has been determined by taking two images with fixed camera (central column). The successful observers could construct a superposition of all of their images after having oriented them (right column).

	Original images in their original orientation	"Double expositions" (Superposition of two images)	Selfmade Transit Series
Altenholz, Germany Rainer Anton
	14:30 UT	13:48 UT	13:37 - 15:00 UT
Bariloche, Argentina Guillermo Abramson
	13:14:59 UT	13:14:59+13:15:59 UT	12:45 - 18:00 UT
Gifhorn, Germany B. Brandt
	12:59:59 UT	12:59:59+13:02:29 UT	12:44:59 - 14:14:58 UT
Medellín, Columbia Enrique Torres
	18:00 UT	17:06 UT + 17:09 UT
Rosario SF, Argentina Aldo Kleiman
	17:00:00 UT	17:00:00+17:02:30 UT	13:00 - 18:00 UT

Combinations of single observations and the resulting solar parallax

If two well oriented images are superimposed which have been taken simultaneously, the resulting picture shows Mercury at slightly different positions of with respect to the sun. This phenomenon is caused by the different distances of Mercury and the sun. Several photos of our participants are of sufficient quality to demonstrate this so-called parallax effect of Mercury. quot;


Parallax effect 13:00 UT Gifhorn, Germany - Bariloche, Argentina measured on this combined images: π_S=12.9"	Parallax effect 13:30 UT Bamberg, Germany - Rosario SF, Argentina measured on this combined images: π_S=13.3"	Parallax effect 13:30 UT Weimar, Germany - Bariloche, Argentina measured on this combined images: π_S=11.7"

	Parallax effect 17:00 UT Medellin, Columbia - Rosario SF, Argentina measured on this combined images: π_S=9.4"

These images show the parallax effect in the correct order of magnitude. But obviously, the derived measures of the solar parallax vary widely. The reason for this problem is that the Mercury's relative positions cannot be measured accurately: Neither the sun's radius, nor the image's orientation and the pixel positions of the sun's and Mercury's centers can be determined exactly.

Observations of the transit by the Solar Dynamics Observatory (SDO)

The influence of the above mentioned uncertainties is the larger the smaller the angle to be measured, i. e., the smaller the distance between the observation sites is. But on earth the distance between this distance cannot be larger than twice the earth's radius R_E. In this situation we were happy to find the photos which had been taken by the Solar Dynamics Observatory (SDO). That telescope is mounted on a satellite moving around the earth on a geosynchronous orbit the radius of which is approximately six times as large as the earth's radius. SDO, therefore, allows us parallax measurements with a baselength of about 6R_E.
In the SDO images the sun's axis of rotation points upwards, i.e., for alignment they must be rotated by about 22.4° counterclockwise.


Superposition of the SDO images taken closest to the proposed times	Rotated to equatorial north and restricted to only one image per point of time	Position results which are used in the following

For our purposes, the SDO images are perfect because they are not influenced by the earth's atmosphere and their orientation is known exactly.

Combination of Mercury's positions as measured from Earth with those captured by the SDO


Gifhorn, Germany - SDO 13:30 UT	Bariloche, Argentina - SDO 14:30 UT

These examples of combinations of project images with those made by SDO show parallactic displacements which are much larger than on the above "earth-bound" pictures generated with photos taken by participants.

The following table shows the results which could be derived by combining complete series of project photos with the according SDO photos. Here, not only the uncertainties of the single comparisons are smaller than those of earth-bound measures, but the series additionally allow statistical analysis and an easy estimation of the standard deviation.

Observers and their locations	Alignments of their series with the SDO series	Resulting measures of the solar parallax	Mean solar parallax and its standard deviation (derived from the line fit values)
Altenholz, Germany Rainer Anton			π_S = 9.1" ± 0.7"
Bariloche, Argentina Guillermo Abramson			π_S = 9.0" ± 0.4"
Daytona Beach, Florida, USA Christian Lockwood			(Somewhat happened with the orientation before 16:00 UT.)
			Restriction to the measures after 16:00 UT leeds us to π_S = 8.4" ± 0.6"
Gifhorn, Germany B. Brandt			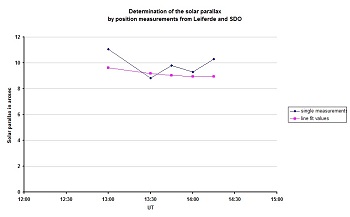π_S = 9.1" ± 0.3"
Medellín, Columbia Enrique Torres			π_S = 10.8" ± 0.5"
Rosario SF, Argentina Aldo Kleiman			π_S = 10.2" ± 0.4"

Final Remarks

Due to our observations and evaluation the parallax of the sun is, with only a small uncertainty, π_S = 9.1", the mean distance d_E between the earth und the sun is, therefore, d_S = R_E/π_S = 22700R_E = 145 000 000 km. Of course, we all knew that already before this project. But now we not only know this measure but also one method of determining it by oneself. And we have got an impression of the difficulties to get a convincing result - even with modern communication and equipment. Edmund Halley got the basic idea of the transit method while observing a transit of Mercury in 1677. For the following generations of astronomers it turned out to be extremely difficult to come to a result (and to reach an agreement). We can now understand why the gathering and the evaluation of the measurements needed decades. "We are standing on the shoulders of giants."

One of our participants, Aldo Kleiman, answered to these remarks as follows: "Beauty may dwell in a sky vista, and even more in a scientific study of a math's formula, beauty dwells without a doubt in the "Transit of Mercury Internet Project." (Thank you!). I remain waiting for the final report."

Here it is.

Navigation