
(this page in Englisch)	(diese Seite auf deutsch)

Los Resultados del Proyecto

A causa de las malas condiciones climáticas en gran parte de Europa y Suramérica durante el tránsito, una gran parte de los participantes no pudo observar el fenómeno ni contribuir con fotografías. Por otra parte, casi todos los aportes tomados cerca de las horas propuestas han seguido el método de exposición múltiple y así se pudo determinar la orientación de las imágenes. La consecuencia es que aun imágenes no muy claras pudieron ser usado para visualizar el efecto paraláctico de mercurio en frente del sol.

Los mejores resultados de los participantes solos/grupos

Las imágenes que siguen muestran los mejores resultados obtenidos de aquellos participantes que han logrado tomar series de imágenes que se han podido alinear. Más resultados se pueden hallar en la página "Primeros Resultados".
Las imágenes de la izquierda son los originales con su orientación. Para poder comparar la posición de Mercurio en frente del sol con otra tomada desde un lugar lejano, es necesario que ambas imágenes tengan exactamente la misma orientación. En este proyecto la orientación este-oeste ha sido determinada tomando dos imágenes con la cámara fija ( se ven en la columna del centro). Las observaciones así orientadas se pueden superponer ( columna de la derecha).

	Imágenes originales (orientación original)	"Exposiciones dobles" (Superposiciones de dos imágenes)	Series caseras del tránsito
Altenholz, Alemania Rainer Anton
	14:30 UT	13:48 UT	13:37 - 15:00 UT
Bariloche, Argentina Guillermo Abramson
	13:14:59 UT	13:14:59+13:15:59 UT	12:45 - 18:00 UT
Gifhorn, Alemania B. Brandt
	12:59:59 UT	12:59:59+13:02:29 UT	12:44:59 - 14:14:58 UT
Medellín, Columbia Enrique Torres
	18:00 UT	17:06 UT + 17:09 UT
Rosario SF, Argentina Aldo Kleiman
	17:00:00 UT	17:00:00+17:02:30 UT	13:00 - 18:00 UT

Combinaciones de observaciones individuales y la paralaje solar obtenido

Cuando se toman simultáneamente dos imágenes desde puntos alejados de la tierra, y estas imágenes son debidamente orientadas y sobreimpuestas, la imágen resultante muestra ligeras variaciones de la posición de Mercurio en frente del sol. Este fenómeno se debe a que el sol y Mercurio se hallan a diferentes distancias de la tierra. Varias de las fotografías de los participantes del proyecto tienen la calidad suficiente para demostrar el llamado "efecto de paralaje" de Mercurio.


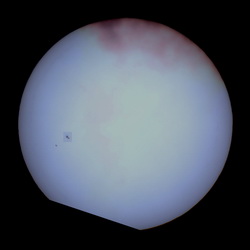Efecto paralláctico 13:00 UT Gifhorn, Alemania - Bariloche, Argentina medido en esta imagen combinada: π_S=12.9"	Efecto paralláctico 13:30 UT Bamberg, Alemania - Rosario SF, Argentina medido en esta imagen combinada: π_S=13.3"	Efecto paralláctico 13:30 UT Weimar, Alemania - Bariloche, Argentina medido en esta imagen combinada: π_S=11.7"

	Efecto paralláctico 17:00 UT Medellin, Columbia - Rosario SF, Argentina medido en esta imagen combinada: π_S=9.4"

Estas imágenes muestran el efecto de paralaje con el debido orden de magnitud. Pero obviamente, las medidas derivadas del paralaje pueden variar considerablemente. La razón de este problema es que es muy difícil medir con la requerida exactitud la posición de Mercurio, el radio solar, la orientación de la imagen y la localización de los centros de los dos cuerpos celestes.

Observaciones del tránsito por el Solar Dynamics Observatory (SDO)

Quanto menor es el ángulo de la paralaje (es decir quanto menor es la distancia entre los lugares) tanto mayor es la influencia de las incertidumbres arriba mencionadas. Pero en la tierra, esta distancia no puede ser mayor que dos veces el radio terrestre R_E. Pero ahora podemos contar con el apoyo de las fotografías tomadas por el SDO. El telescopio está montado en un satélite que orbita alrededor de la tierra en una órbita geoesincrónica cuyo radio es aproximadamende 6 veces el radio de la tierra. SDO, por tanto, permite establecer medidas de paralaje basadas en 6R_E.
En las imágenes del SDO, el eje de rotación solar apunta hacia arriba, por lo que es requerido rotarlas en sentido antihorario 22.4°.


Superposición de las imágenes del SDO hechas alrededor de los tiempos propuestos	rotadas al polo norte y limitadas a una imágen por instante	Posiciones, usadas en lo siguiente

Para nuestros propósitos las imágenes del SDO son perfectas porque no se ven alteradas por la atmósfera terrestre y su orientación se conoce con total exactitud.

Combinaciones de posiciones de Mercurio medidas de la tierra con las observadas por SDO


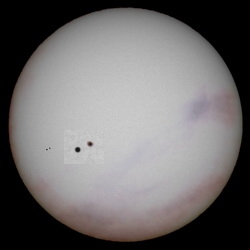Gifhorn, Alemania - SDO 13:30 UT	Bariloche, Argentina - SDO 14:30 UT

Estos ejemplos de combinaciones (por estar basadas en una distancia base mucho mayor) muestran un efecto de paralaje mucho más acentuado que aquellas tommadas solo desde la tierra.

La siguiente tabla muestra los resultados que se pudieron derivar de la combinación de las series completas de fotografías del proyecto con las correspondientes al SDO. En este caso, no sólo las incertidumbres de las comparaciones simples son menores que aquellas effectuadas solo desde la tierra, sino que además se permite incluir un análisis estadístico que arroja como resultado la determinación de la desviación estándard.

Observatores y sus lugares	Alineamiento de sus series con la del SDO	Resultando medidas de la parallaje solar	Parallaje solar medio y su desviación estándar (deducido de las medidas de la linealización)
Altenholz, Alemania Rainer Anton			π_S = 9.1" ± 0.7"
Bariloche, Argentina Guillermo Abramson			π_S = 9.0" ± 0.4"
Daytona Beach, Florida, USA Christian Lockwood			(Antes de 16:00 UT algo pasaba a la orientación de las imágenes.)
			Restricción a las medidas después de 16:00 UT da π_S = 8.4" ± 0.6"
Gifhorn, Alemania B. Brandt			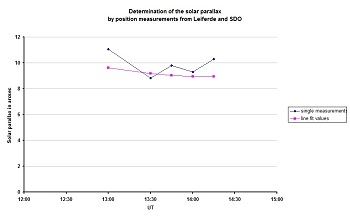π_S = 9.1" ± 0.3"
Medellín, Columbia Enrique Torres			π_S = 10.8" ± 0.5"
Rosario SF, Argentina Aldo Kleiman			π_S = 10.2" ± 0.4"

Comentarios finales

Se ha podido determinar que el paralaje solar es, con una incertidumbre relativamente baja, π_S = 9.1". La distancia media d_E entre el sol y la tierra es, por tanto, d_S = R_E/π_S = 22700R_E = 145 000 000 km. Por supuesto este dato se conocía de antemano. Pero ahora no sólo sabemos el valor sino tambien un método para obtenerlo por nosotros mismos. También nos hemos hecho a una idea de lo complicado que es obtener la información requerida para el cálculo - aún con la communicación y la equipación modernas. Edmund Halley concibió la idea básica del método mientras observaba el tránsito de Mercurio en 1677. Para las siguientes generaciones de astrónomos fue extremadamente difícil obtener un resultado convincente (y no solo eso, sino alcanzar un consenso). Ahora podemos entender porqué el conseguir los datos necesarios requería de décadas de trabajo. "Estamos posados sobre los hombros de gigantes!"

Uno de los participantes, Aldo Kleiman, comentó: "La belleza puede estar en una vista del cielo, y aún más en un estudio científico de una fórmula matemática, pero sin duda ella habita en el proyecto "Tránsito de Mercurio". (Gracias!) Espero con ansia el resultado final."

Aquí está.

¡Muchas gracias a Mauricio Rojas para hacer casí todas las traducciones al español!

Un de nuestros participantes ha publicado un resumen de este proyecto, "La distancia al Sol" en su blog "En el cielo las estrellas". El artículo parece muy digno de leerse.

Navigación